PV - Continuous Compounding
PV with Continuous Compounding Calculator (Click Here or Scroll Down)
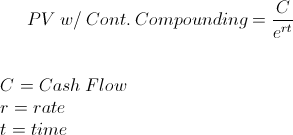
The present value with continuous compounding formula is used to calculate the current value of a future amount that has earned at a continuously compounded rate. There are 3 concepts to consider in the present value with continuous compounding formula: time value of money, present value, and continuous compounding.
Time Value of Money, Present Value, and Continuous Compounding
Time Value of Money - The present value with continuous compounding formula relies on the concept of time value of money. Time value of money is the idea that a specific amount today is worth more than the same amount at a future date. For example, if one were to be offered $1,000 today or $1,000 in 5 years, the presumption is that today would be preferable.
Present Value - The basic premise of present value is the time value of money. To expand upon the prior example, if one were to be offered $1,000 today or $1,250 in 5 years, the answer would not be as obvious as the prior example where both amounts were equal. This is where present value comes in. The offeree would need a way to determine today's value of the future amount of $1,250 to compare the two options.
Continuous Compounding - Continuous Compounding is essentially compounding that is constant. Ordinary compounding will have a compound basis such as monthly, quarterly, semi-annually, and so forth. However, continuous compounding is nonstop, effectively having an infinite amount of compounding for a given time.
The present value with continuous compounding formula uses the last 2 of these concepts for its actual calculations. The cash flow is discounted by the continuously compounded rate factor.
Example of the Present Value with Continuous Compounding Formula
An example of the present value with continuous compounding formula would be an individual who in two years would like to have $1100 in an interest account that is providing an 8% continuously compounded return. To solve for the current amount needed in the account to achieve this balance in two years, the variables are $1,100 is FV, 8% is r, and 2 years is t. The equation for this example would be
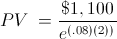
This would return a result of $937.36.
- Formulas related to PV with Continuous Compounding
- Present Value
- Continuous Compounding
- FV - Continuous Compounding
- Annuity - PV w/ Continuous Compounding
- PV - Continuous Compounding Factor