Continuous Compounding
Continuous Compounding Calculator (Click Here or Scroll Down)
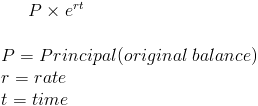
The continuous compounding formula is used to determine the interest earned on an account that is constantly compounded, essentially leading to an infinite amount of compounding periods.
The effect of compounding is earning interest on an investment, or at times paying interest on a debt, that is reinvested to earn additional monies that would not have been gained based on the principal balance alone. By earning interest on prior interest, one can earn at an exponential rate.
The continuous compounding formula takes this effect of compounding to the furthest limit. Instead of compounding interest on an monthly, quarterly, or annual basis, continuous compounding will effectively reinvest gains perpetually.
Example of Continuous Compounding Formula
A simple example of the continuous compounding formula would be an account with an initial balance of $1000 and an annual rate of 10%. To calculate the ending balance after 2 years with continuous compounding, the equation would be
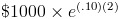
This can be shown as $1000 times e(.2) which will return a balance of $1221.40 after the two years. For comparison, an account that is compounded monthly will return a balance of $1220.39 after the two years. Although the concept of infinite seems that it would return a very large amount, the effect of each compound becomes smaller each time.
How the Continuous Compounding Formula is derived
The continuous compounding formula can be found by first looking at the compound interest formula
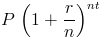
where n is the number of times compounded, t is time, and r is the rate.
When n, or the number of times compounded, is infinite the formula can be rewritten as
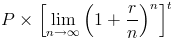
The limit section in the middle of the formula can be shown as er, which leads to the formula at the top of the page.
- Formulas related to Continuous Compounding
- Compound Interest
- Doubling Time - Continuous Compounding
- PV - Continuous Compounding
- FV - Continuous Compounding
- FV of Annuity - Continuous Compounding