PV - Continuous Compounding Factor
PV - Cont. Compounding Factor Calculator (Click Here or Scroll Down)
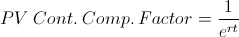
The formula for the present value with continuous compounding factor is used to calculate the present value of $1 received at a future date, discounted on a constant compounding basis. In order to understand the present value with continuous compounding factor formula, it is easier if the different related financial concepts are broken down individually.
Concepts Present Value, Continuous Compounding, and Use of Factors
Present Value - Present Value is a mathematical concept in finance that calculates the current value of an amount received at a future date. This mathematical concept is based on the time value of money, which holds that an amount owned today has a higher value than that same amount received at a future date. In other words, an individual would likely want $100 now and not later. If that individual were to get a promise to receive the money later, they would likely want a premium. A 6% premium, for example, would be $106 a year from now instead of $100 today.
Continuous Compounding - Debts and deposit accounts use various compounding basis when calculating interest. Examples of different compounding basis include simple interest for auto loans, monthly compounding for certificate of deposits (CD's), daily compounding for credit cards. Compounding is when there is additional interest earned on prior interest already earned. For example, if an account has a 1% per month rate. With an initial $100 balance, the account would have $101 after the first month. After the second month, when interest is once again calculated, the balance would be $102.01. The extra $.01 is, in effect, the additional interest earned on $1 of interest earned in the prior month.
With continuous compounding, interest compounding is, in effect, fluid and constant. For the sake of comparison, this .5% effective rate per month, compounded monthly, would result in an ending balance of $106.17. The ending balance of $100, constantly compounded at 6% per year, would result in an ending balance of $106.18.
*Note: Real results may vary due to rounding, fees, et cetera. This illustration is only for educational purposes.
Use of Factors - In financial mathematics, the term "factors" are numerical shortcuts that are intented to simplify a calculation. As stated at the top of the page, the present value with continuous compounding factor is used to calculate the present value of $1 received at a future. By knowing the present value of $1, an individual can calculate any amount by multiplying the amount by the factor for $1. For example, the present value with continuous compounding factor for 6% with a term of 1 is .9418. If one were calculating a $1,000 amount, that individual could multiply the $1,000 amount times .9418 to get a present value with continuous compounding balance of $941.80.
These factors have historically been referenced by individuals in a table format. One axis will represent 't' and the other axis will represent 'r'.
Example of the PV with Continuous Compounding Factor Formula
Suppose that an individual would like to have a $1,000 balance after 3 years, and happens to find an account that has continuous compounding at a rate of 6% per year. This is an unlikely scenario, but is used for the sake of simplicity. The rate 6%, or .06, would be used for the variable 'r'. The variable 't' would be 3. The present value with continuous compounding factor at rate of 6%, and 3 periods, would be .8353. Any amount can be calculated using this factor. For this example though, the $1,000 future value would have a present value of $835.30, which is the present value with continuous compounding factor times $1,000.
Again, actual results may vary due to rounding, fees, leap years, et cetera.
How is the PV with Continuous Compounding Factor Formula Derived?
The present value with continuous compounding factor formula can be found by first looking at the entire formula for PV with continuous compounding
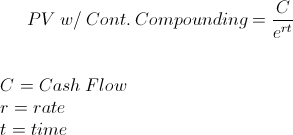
The 'cashflow' or 'payment' variable can be either represented as $1 or factored out of the equation. The result would be the same, as shown at the top of the page.
- Formulas related to PV - Cont. Compounding Factor
- PV - Continuous Compounding