PV of Annuity - Continuous Compounding
PV of Annuity - Cont. Compounding Calculator (Click Here or Scroll Down)
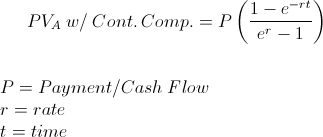
The present value (PV) of an annuity with continuous compounding formula is used to calculate the initial value of a series of a periodic payments when the rate is continuously compounded. The present value of annuity formula when there is continuous compounding contains financial and mathematical concepts that have to be understood individually to understand the entire formula.
Concepts Present Value, Annuity, and Continuous Compounding
Present Value - Present Value is a concept in finance associated with the time value of money. Time value of money holds that a specific amount of money is worth more today than to receive that same amount at a future date. For example, an individual would likely want to receive $100 today than a promise for that same amount a year from now. The formula for present value determines how much the future amount is worth at a prior date based on a specific interest rate.
Annuity - An annuity is a series of periodic payments. An example would be a $100 monthly payment, at 6% interest, for 36 months. This concept, annuity, when combined with the concept of present value, would be considered a decreasing annuity. There is an initial amount, which is the present value, and the balance decreases over time. A real world example would be a loan that has an initial balance, but that balance decreases over time, as payments are made, until the balance is fully paid.
Continuous Compounding - Continuous Compounding is related to an account's compounding basis. Some accounts or debts have simple interest, some are compounded monthly, or compounded daily. With continuous compounding, the account or debt is compounded constantly, instead of periodically. The formula for the PV with continuous compounding of an individual cashflow is
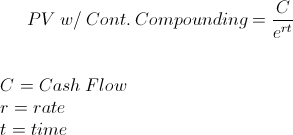
Example of the PV of Annuity with Continuous Compounding Formula
Using the example stated above, suppose a $100 monthly payment, at a .5% nominal rate per month, for 36 months. In order to find the present value of this annuity, assuming there is continuous compounding, we can use the formula at the top of the page to show
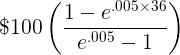
This would return a PV of $32,863.66. This can be checked using the calculator at the bottom of the page.
For the sake of comparison, the same terms without continuous compounding would result in a PV of $32,871.02.
How is the PV of Annuity with Continuous Compounding Formula Derived?
The present value of an annuity is the sum of future cashflows discounted back to their initial value. With continuous compounding, the sum of future cashflows can be shown as
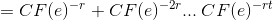
Since the cashflows are all the same, this is considered a geometric series. If we put this into the geometric series formula, this would show
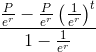
This equation can be multiplied by er/er, which is to multiply it by 1. By doing this, er is now elimated throughout the formula to now show

The payment, P, in the formula directly above can be factored out which will result in the formula at the top of the page.
- Formulas related to PV of Annuity - Cont. Compounding
- PV of Annuity
- Continuous Compounding
- PV - Continuous Compounding
- Annuity - FV w/ Continuous Compounding