Doubling Time - Continuous Compounding
Doubling Time Continuous Compounding Calculator (Click Here or Scroll Down)
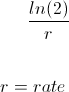
The doubling time formula with continuous compounding is the natural log of 2 divided by the rate of return.
The formula for doubling time with continuous compounding is used to calculate the length of time it takes doubles one's money in an account or investment that has continuous compounding.
It is important to note that this formula will return a time to double based on the term of the rate. For example, if the monthly rate is used, the answer to the formula will return the number of months it takes to double. If the annual rate is used, the answer will then reflect the number of years to double.
Example of the Doubling with Continuous Compounding Formula
An example of the doubling time with continuous compounding formula is an individual would like to calculate how long it would take to double his investment that earns 6% per year, continuously compounded. The individual could either calculate the number of years or calculate the number of months to double his investment by using the annual rate or the monthly rate. Using the doubling time for continuous compounding formula, the time to double at a rate of 6% per year would show
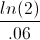
This equation would return a result of 11.55 years.
How is the Doubling Time with Continuous Compounding Formula derived?
The doubling time with continuous compounding formula can be found by first looking at the continuous compounding formula individually.

FV is the future value and PV is the present value. To double one's money would be to have the future value equal to twice the amount of the present value. Considering this, we can substitute 2 for FV and 1 for PV in the formula above. This would show

This formula can be adjusted as
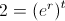
Since we are solving for t, this formula can be rewritten as
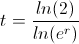
The denominator of the formula above becomes simply r, which is the formula shown at the top of the page.
- Formulas related to Doubling Time - Continuous Compounding
- Doubling Time
- Continuous Compounding
- Doubling Time - Simple Interest