Annuity (FV)- Solve for n

Solve for n on Annuity - (FV) Calculator (Click Here or Scroll Down)

Solve for Number of Periods on Annuity (FV)

The formula for solving for number of periods (n) on an annuity shown above is used to calculate the number of periods based on the future value, rate, and periodic cash flows.

The formula at the top of the page, solving for n, generally approaches the question "How long will it take to save $x amount dollars by saving $y per month at a rate of z%".

Example of Solve for n on Annuity Formula

Suppose that an individual receives an additional $1000 pay or bonus semiannually. Suppose this individual would like to find out how long until they save $19600 by saving $1,000 every half year at an effective rate of 5% every half year. **It is important to remember that the rate should match the frequency of the cash flows/payments. For example, if cash flows are semi-annual, then the effective semi-annual rate is used. The term effective implies that compounding is already adjusted for that period (see effective rate).

Using the formula at the top of the page to solve for the number of periods, n, for this example would show the equation

Example solving for n

The above equation can be reduced to

Example of Solving for n reduced

which results in 14 semi-annual periods.

*Note that this is for academic reasons only. Actual results may vary due to fees, exact cash flow dates, et cetera
**See section labeled Alternative Method for an additional way of solving this example.

How is the Solve for n on Annuity Formula Derived?

Solving for the number of periods on an annuity requires first looking the future value of annuity formula.

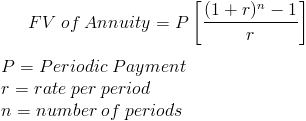
FV of Annuity

The number of periods can be found by rearranging the above formula to solve for n. The first step would be to multiply both sides by r/P. Then we can add 1 to each side which all results in the following formula

FV of Annuity Rearranged

From here it is seen that (1+r)n is isolated on the right side of the equation. To solve for the exponent n requires taking the ln of both sides of the equation.The equation directly above can be reduced to

Solving for Number of Periods continued

Both sides of the equation above can be divided by ln(1+r) which would result in the formula at the top of the page, solving for n.

Alternative method to Solve for Number of Periods n

Another method of solving for the number of periods (n) on an annuity based on future value is to use a future value of annuity (or increasing annuity) table. Solving for the number of periods can be achieved by dividing FV/P, the future value divided by the payment. This result can be found in the "middle section" of the table matched with the rate to find the number of periods, n.

For example, using the example provided in the preceding section, the future value of $19600 can be divided by semi-annual cash flows of $1,000 which results in 19.6. Using the future value of annuity table, one can see that at an effective rate of 5%, 19.6 in the table matches up to 14 (semi-annual) periods.


Return to Top


New to Finance?

Start with the Basics

Annuity (FV) - Solve for n Calculator