Weighted Average Cost of Capital Formula (with Calculator)

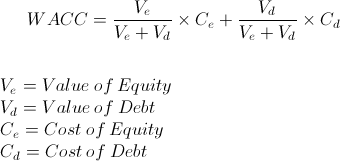
The weighted average cost of capital (WACC) is the average cost that a company has incurred or will incur for access to capital. If a company is considering an additional project, it may use this formula to look at what the new WACC would be based on a change in the company's capital structure (i.e., the costs may change, and the weights will likely change, and so a new WACC is calculated). Whether you use the past information or future information for each variable in the formula largely depends on the reason to gather this information. Future considerations require future data, present considerations require present data, and historical considerations require past data.

The weighted average cost of capital is calculated by multiplying the weight of each source of capital by its cost, then adding these results together.

The weighted average cost of capital uses three financial and math concepts: weighted average, cost of equity, and cost of debt. To understand WACC, one needs to first understand what weighted average is, and understand each one of these sources of capital that are weighted.

Weighted Average

The general weighted average formula is shown as:

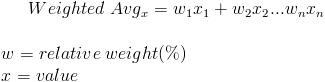
Weighted average is used in various financial formulas. Examples include the formula listed at the top of this page, portfolio beta, forecasting earnings, and forecasting returns.

To best illustrate weighted average, one needs to first look at arithmetic mean. Arithmetic mean is what people are referring to when they speak of the average of something. For example, the average of 2 and 4 is 3. This is found by adding 2 and 4, then dividing the result, 6, by the quantity of 2.

In contrast to the arithmetic mean, the weighted average puts different weights on each variable being considered. This may be necessary for various reasons, but typically, different weights are used due to there being unequal proportions for each variable. For example, using the prior example, suppose that an individual gets 2 80% of the time and 4 for the remaining 20% of the time. Obviously, the arithmetic mean has no use for this scenario and does not represent an actual average. The weighted average would be 2.4. In 100 examples, 80 would give a result of 2 and 20 would give a result of 4, which averages to 2.4 over the 100 examples.

Cost of Debt

One source of capital for a company is to take on new debt. A company may use the rate the company pays on new debt for the cost of debt or may use an average of all debt. What is important, is to use whatever method that is relevant to the analysis.

Proper analysis also requires looking at the tax considerations of debt versus equity. If a company can reduce their taxes by deducting debt from revenues, then a proper comparison would require looking at the 'after-tax cost of debt'. This can be calculated by multiplying the cost of debt by (1-t), with t being the marginal tax rate. This changes the cost of debt to:

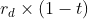
See the alternative formula listed at the bottom of this page.

If a company has no debt, the WACC is equal to the cost of equity. The weight of debt would effectively be zero and the weight of equity would be 1.0, or 100%. In this case, the formula would show the cost of equity multiplied by 1.0, which leaves it unaffected.

Cost of Equity

Another source of capital for a company is to issue new equity. The 'cost of equity' referenced in the WACC formula, is the required return on the company's stock by investors.

One method of calculating the required return on a company's stock, is the capital asset pricing model (CAPM). The capital asset pricing model calculates a company's required return by comparing the market's risk and return to the company's risk in order to come up with a return. This is shown by the following formula:

where the risk-free rate is added to the product of the company's beta and the risk premium. The risk premium is the average return on the market minus the risk-free rate.

Another method of calculating the cost of equity for a company with constant growth and dividends, is to use its dividend yield and growth rate. If the valuation of a company with constant growth is:

then the required return can be determined by rearranging the formula as:

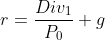
which is the dividend yield added to the growth rate.

Note: The costs associated with issuing new equity would need to be considered and adjusted, in the same way as tax deductions are considered in the cost of debt.

How to Determine Weights

The weights of each source of capital can be calculated as its portion of all capital. For example, suppose that there are two sources being considered, debt and equity. The weight of debt would be the proportion of debt in relation to the sum of both debt and equity. This part of the WACC is shown as:

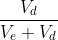
As with any time someone is using weighted average, all weights must add up to 1. The number 1 represents 100%, and 100% of all data needs to be considered for an accurate result. For example, assume debt and equity are the only two sources of capital. If debt makes up 40% of the total capital, equity must necessarily be 60% of total capital.

As mentioned in the first section of this page, whether to use past data, present data, or future data depends on the analysis. A company considering future sources of capital will likely calculate the new weights (as well as changes in the cost) after the change.

Additional Sources of Capital

A company may consider additional sources of capital besides common equity and debt. Examples include retained earnings, warrants and preferred stock.

If additional sources of capital are being considered, then the cost of each source of capital needs to be taken into consideration in the same way equity and debt is. The weight of each source needs to be considered along with the cost of each source of capital.

Use of the Weighted Average Cost of Capital Formula

The formula for WACC is used internally by companies for capital budgeting. More specifically, a company may need to look at the best capital mix in order to reduce the company's WACC. A company may utilize one source over the other, in order to reduce the overall weighted average.

A company may also look at the WACC when considering new projects. If a project has a return of 10% but the cost of capital is 11%, this would be a net negative for the entire company.

Examples of the WACC Formula

1.A simple example of the weighted average cost of capital would be to suppose that a company is considering a new project and is evaluating two different capital structures.

Scenario A has a 20% proportion of debt and 80% proportion of equity. The cost of debt is 5% and the cost of equity is 10%.

Scenario B has a 40% proportion of debt and 60% proportion of equity. The cost of debt is 6% and the cost of equity is 12%.

Putting these variables into the weighted average cost of capital formula would show

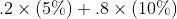
for scenario A and Scenario B would show

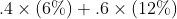
Scenario A would have an WACC of 9% and Scenario B would have an WACC of 9.6%.

2.To expand on the prior example, suppose that a company has a market cap of $60 million and debt totaling $20 million. The rate on the debt is 8% and the marginal tax rate for the company is 30%. We can see that value of equity and debt combined is $80 million. The weight of equity would be .75, which is $60 million divided by $80 million. The remaining .25 weight would be used for debt, which can be confirmed by dividing $20 million by $80 million.

The after-tax cost of debt can be calculated as (See the Alternative WACC Formula in the following section and Cost of Debt section for formula):

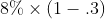
which results in an after-tax cost of debt of 5.6%.

Let us also assume that the company has a beta of 1.4, the market rate is 8% and the risk-free rate is 2%. Using CAPM, we can calculate the required return:

which results in a cost of equity of 10.4%.

To recap, we have a weight of debt of .25 with an after-tax cost of 5.6%. We also have a weight of equity of .75 and a cost of equity of 10.4%. Putting these variables into the WACC formula shows

which results in an WACC of 9.2%.

Alternative WACC Formula

The formula for the weighted average cost of capital may also be shown as:

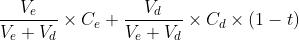
This formula simply restates the formula at the top of the page but emphasizes the need to adjust the before-tax cost of debt to an after-tax cost of debt.

Return to Top

Weighted Average Cost of Capital