Growing Annuity Payment - PV
Growing Annuity Payment Calculator (PV) (Click Here or Scroll Down)

The growing annuity payment from present value formula shown above is used to calculate the initial payment of a series of periodic payments that grow at a proportionate rate. This formula is used specifically when present value is known.
A growing annuity is an annuity where the payments grow at a particular rate. For example, assume that the initial payment is $100 and the payments are expected to grow each period at 10%. As stated, the first payment is $100, then the second payment would be $110 ($100 x [1 + g]), and the third payment would be $121 ($110 x [1 + g]).
It is important to keep in mind that the formula shown above will only calculate the first payment.
How is the Growing Annuity Payment Formula using Present Value Derived?
The formula for calculating the initial payment on a growing annuity is found by rearranging the present value of a growing annuity formula
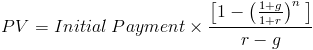
The initial payment can be calculated by dividing both sides by the second portion of the formula shown directly above, which can be shown as

This leaves the initial payment equal to the present value divided by this second section. This can then be further simplified by multiplying PV times the reciprocal of the denominator, which will return the formula shown at the top of the page.
Calculating a Future Payment for a Growing Annuity
The payment at a future date can be calculated using the following formula

Using the prior example in the first section, an initial payment of $100 at a growth rate of 10% would have a third payment of $121. This can be calculated by multiplying $100 by (1+g)2.
Alternative Growing Annuity Payment Formula using Present Value

The formula for calculating the initial payment on a growing annuity and the formula for calculating a future payment can be combined to give a complete formula for calculating a payment at time t.
- Formulas related to Growing Annuity Payment (PV)
- Growing Annuity - PV
- Growing Annuity Payment (FV)