Present Value of a Growing Annuity
PV of a Growing Annuity Calculator (Click Here or Scroll Down)
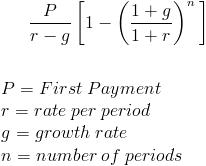
The present value of a growing annuity formula calculates the present day value of a series of future periodic payments that grow at a proportionate rate. A growing annuity may sometimes be referred to as an increasing annuity. A simple example of a growing annuity would be an individual who receives $100 the first year and successive payments increase by 10% per year for a total of three years. This would be a receipt of $100, $110, and $121, respectively.
The present value of a growing annuity formula relies on the concept of time value of money. The premise to this concept is that a specific quantity of money is worth more today than at a future time.
Like all financial formulas that involve a rate, it is important to correlate the rate per period to the number of periods in the present value of a growing annuity formula. If the payments are monthly, then the rate would need to be the monthly rate.
How is the Present Value of a Growing Annuity Derived?
The present value of a growing annuity is the sum of future cash flows. For a growing annuity, each cash flow increases at a certain rate. The formula for the present value of a growing annuity can be written as
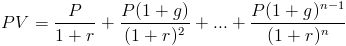
This formula is the general formula for summing the discounted future cash flows along with using 1 + g to factor in that each future cash flow will increase at a specific rate.
This present value of a growing annuity formula can then be rewritten as
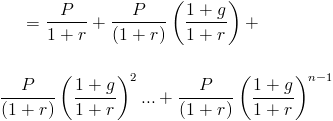
This would be considered a geometric series where (1+g)/(1+r) is the common ratio. By using the geometric series formula, the present value of a growing annuity will be shown as
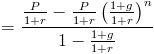
This formula can be simplified by multiplying it by (1+r)/(1+r), which is to multiply it by 1. This cancels out many of these throughout the formula, which leaves
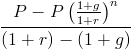
In the denominator, (1+r) - (1+g) will return r-g. At this point, P and r-g can be factored out, which will lead to the present value of a growing annuity formula shown at the top of the page.
- Formulas related to PV of a Growing Annuity
- PV of Annuity
- PV of Growing Perpetuity
- Growing Annuity - Payment (PV)
- FV of Growing Annuity