Doubling Time
Doubling Time Calculator (Click Here or Scroll Down)

The Doubling Time formula is used in Finance to calculate the length of time required to double an investment or money in an interest bearing account.
It is important to note that r in the doubling time formula is the rate per period. If one wishes to calculate the amount of time to double their money in a money market account that is compounded monthly, then r needs to express the monthly rate and not the annual rate. The monthly rate can be found by dividing the annual rate by 12. With this situation, the doubling time formula will give the number of months that it takes to double money and not years.
In addition to expressing r as the monthly rate if the account is compounded monthly, one could also use the effective annual rate, or annual percentage yield, as r in the doubling time formula.
Example of Doubling Time Formula
Jacques would like to determine how long it would take to double the money in his money market account. He is earning 6% per year, which is compounded monthly. Looking at the doubling time formula, we need to consider that the 6% would need to be divided by 12 in order to come to a monthly rate since the account is compounded monthly. Given this, r in the doubling time formula would be .005 (.06/12). After putting this into the doubling time formula, we have:
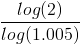
After solving, the doubling time formula shows that Jacques would double his money within 138.98 months, or 11.58 years.
As stated earlier, another approach to the doubling time formula that could be used with this example would be to calculate the annual percentage yield, or effective annual rate, and use it as r. The annual percentage yield on 6% compounded monthly would be 6.168%. Using 6.168% in the doubling time formula would return the same result of 11.58 years.
Alternative to Doubling Time
For quick estimations of how long it takes to double the money on an investment, some may choose to use the rule of 72. The rule of 72 is found by dividing 72 by the rate of interest expressed as a whole number. For example, a rate of 6% would be estimated by dividing 72 by 6 which would result in 12 years. As stated, this is only an estimation as a 6% rate would take 11.90 years using the actual doubling time formula.
- Formulas related to Doubling Time
- Rule of 72
- Doubling Time - Continuous Compounding
- Doubling Time - Simple Interest
- Solve for Number of Periods - PV&FV